接雨水

接雨水

题目描述

原题链接：42. 接雨水 - 力扣（LeetCode）

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

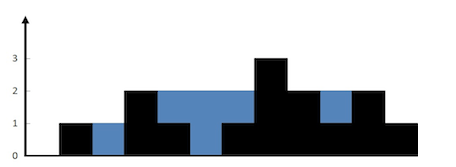
image-20230703085843447

1
2
3
输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例 2：

1
2
输入：height = [4,2,0,3,2,5]
输出：9

提示：

  • n == height.length

  • 1 <= n <= 2 * 104

  • 0 <= height[i] <= 105

解题思路

三种思路：

  1. 按列思考（纯暴力），思考每一列可以接多少雨水；

    具体实现思路，从第二列开始向左找最高的柱子并记录高度tmp_l，并且向右找最高的柱子记录高度tmp_r，记录当前列柱子高度为tmp，那么当前列接雨水的数量ans=min(tmp_l，tmp_r) - tmp;

  2. 按行（栈）思考，匹配两个柱子之间所占行的雨水数；

  3. dp优化方法1，定义集合f_l[i]代表第 i 列左边最高的墙的高度，f_r[i]代表第 i列右边最高的墙的高度，构建如上集合后，用法1解。

    状态转移方程：

    • f_l[i] = max(f_l[i-1], height[i-1])
    • f_r[i] = max(f_r[i+1], height[i+1])

  4. 堆思路（木桶效应）：

    我们可以先让两边的端点入堆，然后弹出较小者，并检查其左（或右）的高度是否比它小，如果比它小，说明可以注水，那么，我们就把它注水到相同的高度，并将注水后的高度入堆，如果比它高，直接入堆，依次进行下去，最终，总的注水量就是接雨水的量。

    当然，这里为了防止重复访问每个坐标，我们使用一个 si 变量记录已经访问过的坐标。

代码

  1. 纯暴力
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int trap(int[] height) {
        int n = height.length;
        int ans = 0;
        for(int i = 1; i < n - 1; i++){
            int tmp = height[i], tmp_l = tmp, tmp_r = tmp;
            for(int j = i - 1; j >= 0 ; j--){
                if(tmp_l <= height[j]){
                    tmp_l = height[j];
                }
            }
            for(int j = i + 1; j < n; j++){
                if(tmp_r <= height[j]){
                    tmp_r = height[j];
                }
            }
            if(tmp <= tmp_l && tmp <= tmp_r)ans += Math.min(tmp_l, tmp_r) - tmp;
        }
        return ans;
    }
}

AC记录：

image-20230703090848027

可以看出来，暴力的效率很差。

  1. 按行思考，考虑用栈来处理，入栈策略为：
  • 当前高度小于等于栈顶高度，入栈，指针后移。
  • 当前高度大于栈顶高度，出栈，计算出当前墙和栈顶的墙之间水的多少，然后计算当前的高度和新栈的高度的关系，重复当前的步骤。直到当前墙的高度不大于栈顶高度或者栈空，然后把当前墙入栈，指针后移。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public int trap(int[] height) {
        // 柱子的数量
        int n = height.length;
        // 雨水的数量
        int ans = 0;
        Stack<Integer> s = new Stack<>();
        s.push(0);
        for(int i = 1; i < n; i++){
            int tmp_r = height[i], tmp_s = height[(int)s.peek()];
            while(tmp_r > tmp_s && !s.empty()){
                s.pop();
                if(s.empty())
                    break;
                int j = (int)s.peek();
                int tmp_l = height[j];
                int d = i - j - 1;
                ans += (Math.min(tmp_l, tmp_r) - tmp_s) * d;
                tmp_s = tmp_l;

            }
            s.push(i);
        }
        return ans;
    }
}

AC记录：

image-20230703214102148

这种方法快了很多嘿嘿嘿。

  1. dp优化方法1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int trap(int[] height) {
        // 柱子的数量
        int n = height.length;
        int ans = 0;
        int[] f_l = new int[n + 10];
        int[] f_r = new int[n + 10];
        for(int i = 1; i < n; i++){
            f_l[i] = Math.max(f_l[i-1], height[i-1]);
        }
        for(int i = n - 2; i >= 0; i--){
            f_r[i] = Math.max(f_r[i+1], height[i+1]);
        }
        for(int i = 1; i < n; i++){
            int min = Math.min(f_l[i], f_r[i]);
            if(min > height[i])
            ans += min - height[i];
        }
        return ans;
    }
}

AC记录：

image-20230703215921047

比栈还要快！！！

众所周知，dp可以用滚动数组优化，但是这里有两个dp，我们选择优化其中一个，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public int trap(int[] height) {
        // 柱子的数量
        int n = height.length;
        int ans = 0;
        int f_l = 0;
        int[] f_r = new int[n + 10];
        for(int i = n - 2; i >= 0; i--){
            f_r[i] = Math.max(f_r[i+1], height[i+1]);
        }
        // 优化了左边最大值的寻找
        for(int i = 1; i < n; i++){
            f_l = Math.max(f_l, height[i-1]);
            int min = Math.min(f_l, f_r[i]);
            if(min > height[i])
            ans += min - height[i];
        }
        return ans;
    }
}

AC记录：

image-20230703220615238

感觉效率没什么变化。

  1. 堆：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {

    int[] dirs = {-1, 1};

    public int trap(int[] height) {
        // 用优先队列解决，保存<位置,高度>
        int n = height.length;
        boolean[] si = new boolean[n];
        si[0] = si[n - 1] = true;
        // 上述语句在Java中创建了一个优先队列（PriorityQueue）的实例对象，该优先队列按照传入的比较器（Comparator）来确定元素的优先级。比较器使用了lambda表达式 (a, b) -> a[1] - b[1]，表示比较元素数组的索引为1的元素的大小。元素类型为int数组（int[]）。

        // 换句话说，这个优先队列会根据int数组中索引为1的元素的大小来确定元素的优先级，其中较小的元素会被放置在队列的前面。
        PriorityQueue<int[]> heap = new PriorityQueue<>((a,b)->a[1]-b[1]);
        // 初态把第一个元素和最后一个元素放进去
        heap.offer(new int[] {0, height[0]});
        heap.offer(new int[] {n - 1, height[n - 1]});

        int ans = 0;
        while (!heap.isEmpty()) {
            // 取出当前最小的柱子的下标并出队
            int[] element = heap.poll();
            // 看看左右两边的情况
            for (int dir : dirs) {
                int pos = element[0] + dir;
                if (pos >= 0 && pos < n && !si[pos]) {
                    // 如果当前高度左或右的高度小于当前高度
                    if (height[pos] < element[1]) {
                        // 计算左或右列的水量
                        ans += element[1] - height[pos];
                    }
                    // 比较当前和左或者右列的高度，并让最大高度与当前位置入队
                    heap.offer(new int[] {pos, Math.max(height[pos], element[1])});
                    // 标记位置
                    si[pos] = true;
                }
            }
        }

        return ans;
    }
}

AC记录：

image-20230704214748751

emm，至此此题结束啦！！！(>.<完结撒花)

刷题 > dp
#刷题 #dp #暴力 #栈 #堆
接雨水
http://example.com/2023/07/03/接雨水/
作者
子川
发布于
2023年7月3日
许可协议